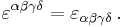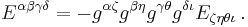Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus. It is named after the Italian mathematician and physicist Tullio Levi-Civita.
Contents |
Definition
In three dimensions, the Levi-Civita symbol is defined as follows:
i.e. 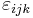 is 1 if (i, j, k) is an even permutation of (1,2,3), −1 if it is an odd permutation, and 0 if any index is repeated.
is 1 if (i, j, k) is an even permutation of (1,2,3), −1 if it is an odd permutation, and 0 if any index is repeated.
The formula for the three dimensional Levi-Civita symbol is:
The formula in four dimensions is:
For example, in linear algebra, the determinant of a 3×3 matrix A can be written
(and similarly for a square matrix of general size, see below)
and the cross product of two vectors can be written as a determinant:
or more simply:
According to the Einstein notation, the summation symbols may be omitted.
The tensor whose components in an orthonormal basis are given by the Levi-Civita symbol (a tensor of covariant rank n) is sometimes called the permutation tensor. It is actually a pseudotensor because under an orthogonal transformation of jacobian determinant −1 (i.e., a rotation composed with a reflection), it acquires a minus sign. Because the Levi-Civita symbol is a pseudotensor, the result of taking a cross product is a pseudovector, not a vector.
Note that under a general coordinate change, the components of the permutation tensor get multiplied by the jacobian of the transformation matrix. This implies that in coordinate frames different from the one in which the tensor was defined, its components can differ from those of the Levi-Civita symbol by an overall factor. If the frame is orthonormal, the factor will be ±1 depending on whether the orientation of the frame is the same or not.
Relation to Kronecker delta
The Levi-Civita symbol is related to the Kronecker delta. In three dimensions, the relationship is given by the following equations:
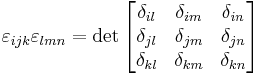
-
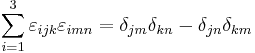 ("contracted epsilon identity")
("contracted epsilon identity")
In Einstein notation, the duplication of the i index implies the sum on i. The previous is then denoted: 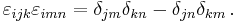
Generalization to n dimensions
The Levi-Civita symbol can be generalized to higher dimensions:
Thus, it is the sign of the permutation in the case of a permutation, and zero otherwise.
Some generalized formulae are:
where n is the dimension (rank), and
where G(n) is the Barnes G-function.
For any n, the property
follows from the facts that (a) every permutation is either even or odd, (b) (+1)2 = (-1)2 = 1, and (c) the permutations of any n-element set number exactly n!.
In index-free tensor notation, the Levi-Civita symbol is replaced by the concept of the Hodge dual.
In general, for n dimensions, one can write the product of two Levi-Civita symbols as:
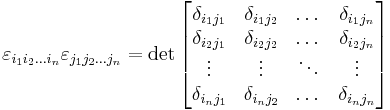 .
.
Properties
(in these examples, superscripts should be considered equivalent with subscripts)
1. In two dimensions, when all 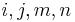 are in
are in 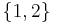 ,
,
2. In three dimensions, when all 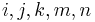 are in
are in 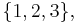
3. In n dimensions, when all 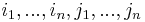 are in
are in 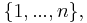 :
:
Proofs
For equation 1, both sides are antisymmetric with respect of 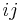 and
and 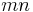 . We therefore only need to consider the case
. We therefore only need to consider the case 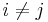 and
and 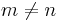 . By substitution, we see that the equation holds for
. By substitution, we see that the equation holds for 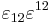 , i.e., for
, i.e., for 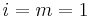 and
and 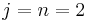 . (Both sides are then one). Since the equation is antisymmetric in
. (Both sides are then one). Since the equation is antisymmetric in 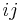 and
and 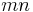 , any set of values for these can be reduced to the above case (which holds). The equation thus holds for all values of
, any set of values for these can be reduced to the above case (which holds). The equation thus holds for all values of 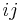 and
and 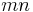 . Using equation 1, we have for equation 2
. Using equation 1, we have for equation 2 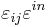

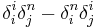
-

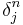 .
.
Here we used the Einstein summation convention with  going from
going from 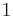 to
to 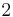 . Equation 3 follows similarly from equation 2. To establish equation 4, let us first observe that both sides vanish when
. Equation 3 follows similarly from equation 2. To establish equation 4, let us first observe that both sides vanish when 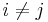 . Indeed, if
. Indeed, if 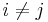 , then one can not choose
, then one can not choose  and
and  such that both permutation symbols on the left are nonzero. Then, with
such that both permutation symbols on the left are nonzero. Then, with 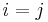 fixed, there are only two ways to choose
fixed, there are only two ways to choose  and
and  from the remaining two indices. For any such indices, we have
from the remaining two indices. For any such indices, we have 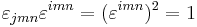 (no summation), and the result follows. Property (5) follows since
(no summation), and the result follows. Property (5) follows since 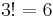 and for any distinct indices
and for any distinct indices 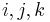 in
in 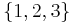 , we have
, we have 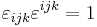 (no summation).
(no summation).
Examples
1. The determinant of an 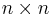 matrix
matrix 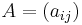 can be written as
can be written as
where each 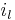 should be summed over
should be summed over 
Equivalently, it may be written as
where now each 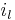 and each
and each 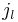 should be summed over
should be summed over  .
.
2. If 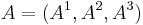 and
and 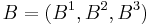 are vectors in
are vectors in 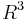 (represented in some right hand oriented orthonormal basis), then the
(represented in some right hand oriented orthonormal basis), then the  th component of their cross product equals
th component of their cross product equals
For instance, the first component of 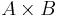 is
is 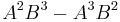 . From the above expression for the cross product, it is clear that
. From the above expression for the cross product, it is clear that 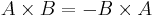 . Further, if
. Further, if 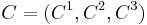 is a vector like
is a vector like  and
and  , then the triple scalar product equals
, then the triple scalar product equals
From this expression, it can be seen that the triple scalar product is antisymmetric when exchanging any adjacent arguments. For example, 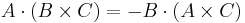 .
.
3. Suppose 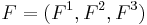 is a vector field defined on some open set of
is a vector field defined on some open set of 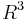 with Cartesian coordinates
with Cartesian coordinates 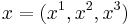 . Then the
. Then the  th component of the curl of
th component of the curl of  equals
equals
Notation
A shorthand notation for anti-symmetrization is denoted by a pair of square brackets. For example, in arbitrary dimensions, for a rank 2 covariant tensor M,
and for a rank 3 covariant tensor T,
In three dimensions, these are equivalent to
While in four dimensions, these are equivalent to
More generally, in n dimensions
Tensor density
In any arbitrary curvilinear coordinate system and even in the absence of a metric on the manifold, the Levi-Civita symbol as defined above may be considered to be a tensor density field in two different ways. It may be regarded as a contravariant tensor density of weight +1 or as a covariant tensor density of weight -1. In four dimensions,
Notice that the value, and in particular the sign, does not change.
Ordinary tensor
In the presence of a metric tensor field, one may define an ordinary contravariant tensor field which agrees with the Levi-Civita symbol at each event whenever the coordinate system is such that the metric is orthonormal at that event. Similarly, one may also define an ordinary covariant tensor field which agrees with the Levi-Civita symbol at each event whenever the coordinate system is such that the metric is orthonormal at that event. These ordinary tensor fields should not be confused with each other, nor should they be confused with the tensor density fields mentioned above. One of these ordinary tensor fields may be converted to the other by raising or lowering the indices with the metric as is usual, but a minus sign is needed if the metric signature contains an odd number of negatives. For example, in Minkowski space (the four dimensional spacetime of special relativity)
Notice the minus sign.
See also
References
- Charles W. Misner, Kip S. Thorne, John Archibald Wheeler, Gravitation, (1970) W.H. Freeman, New York; ISBN 0-7167-0344-0. (See section 3.5 for a review of tensors in general relativity).
This article incorporates material from Levi-Civita permutation symbol on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
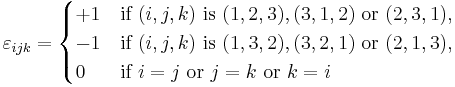
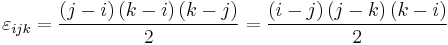
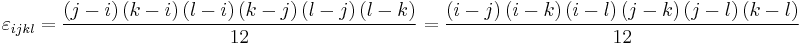
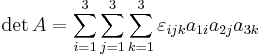
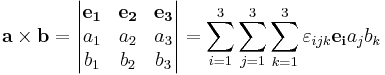
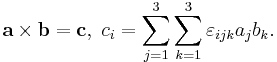
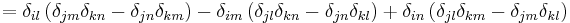
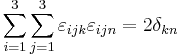
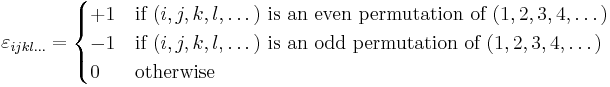
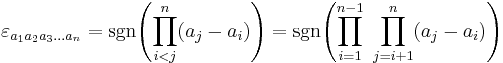
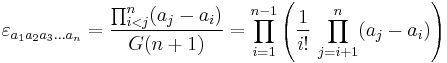
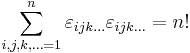
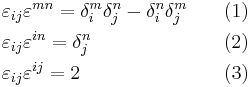
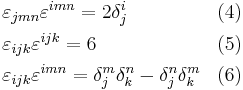
![\begin{align}& \varepsilon_{i_1 \dots i_n} \varepsilon^{j_1 \dots j_n} = n! \delta^{j_1}_{[ i_1} \dots \delta^{j_n}_{i_n ]} &&(7)\\& \varepsilon_{i_1 \dots i_k~i_{k%2B1}\dots i_n} \varepsilon^{i_1 \dots i_k~j_{k%2B1}\dots j_n}= k!(n-k)!~\delta^{j_{k%2B1}}_{[ i_{k%2B1}} \dots \delta^{j_n}_{i_n ]} &&(8)\\& \varepsilon_{i_1 \dots i_n}\varepsilon^{i_1 \dots i_n} = n! &&(9)\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/5335c8273749de494f2352a5f8bcc885.png)
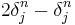
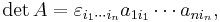
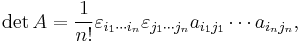
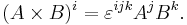
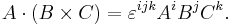
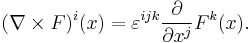
![M_{[ab]} = \frac{1}{2!}(M_{ab} - M_{ba}) \,,](/2012-wikipedia_en_all_nopic_01_2012/I/5b9aaf5af32efb15f99715b29fbaf947.png)
![T_{[abc]} = \frac{1}{3!}(T_{abc}-T_{acb}%2BT_{bca}-T_{bac}%2BT_{cab}-T_{cba}) \,.](/2012-wikipedia_en_all_nopic_01_2012/I/28702592446377621d6ba2be5bac035c.png)
![M_{[ab]} = \varepsilon_{abc} \, \frac{1}{2!} \, \varepsilon^{dec} M_{de} \,,](/2012-wikipedia_en_all_nopic_01_2012/I/5077c9c0699fe4a61b45e672b4ae5003.png)
![T_{[abc]} = \varepsilon_{abc} \, \frac{1}{3!} \, \varepsilon^{def} T_{def} \,.](/2012-wikipedia_en_all_nopic_01_2012/I/f7a2fdf9c5917dcd4cd2950d2fb3f01e.png)
![M_{[ab]} = \frac{1}{2!} \, \varepsilon_{abcd} \, \frac{1}{2!} \, \varepsilon^{efcd} M_{ef} \,,](/2012-wikipedia_en_all_nopic_01_2012/I/4dc57a1820125dddb0942013abb47107.png)
![T_{[abc]} = \varepsilon_{abcd} \, \frac{1}{3!} \, \varepsilon^{efgd} T_{efg} \,.](/2012-wikipedia_en_all_nopic_01_2012/I/822b50bc406da096fd87e8071e915986.png)
![S_{[a_1 \dots a_i]} = \frac{1}{(n-i)!} \varepsilon_{a_1 \dots a_i~b_1 \dots b_{n-i}} \frac{1}{i!} \varepsilon^{c_1 \dots c_i~b_1 \dots b_{n-i}} S_{c_1 \dots c_i} \,.](/2012-wikipedia_en_all_nopic_01_2012/I/3af8846ce86a1e73a3559054cbc0a0e8.png)